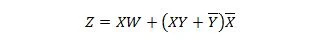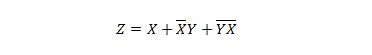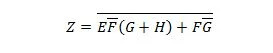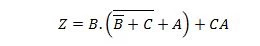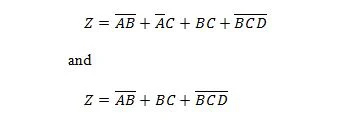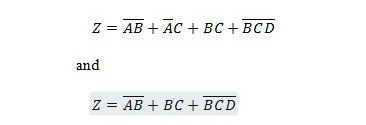Глава 2: Булева алгебра и свързаните с нея компютърни компоненти

Глава 2: Булева алгебра и свързаните с нея компютърни компоненти

2.1 Основни булеви оператори

Да приемем, че аз (авторът) съм висок и вие (читателят) сте високи. Ако някой ви попита дали и двамата сме високи, ще кажете „Да“ (вярно). Ако той попита дали и двамата сме ниски, ще кажете „Не“ (невярно). Ако ти си нисък, а аз съм висок и той те попита дали ти или аз сме високи, отговорът ти ще бъде „Да“ (вярно). Ако той попита дали и ти, и аз сме високи, няма да имаш отговор. Може да продължите да кажете, че последният въпрос не трябва да се задава или че въпросът няма отговор. Е, искам ти (читателят) да знаеш, че днес, при определени обстоятелства, трябва да се зададе въпросът.

В биологията човек е или висок, или нисък. Условията на „околната среда“ са тези, които карат човека да има среден ръст. Един учен, Джордж Бул, дефинира набор от отговори или правила за този вид въпроси. Ще научим тези правила в този раздел на онлайн курса за кариера (глава). Тези правила се използват в компютрите, програмирането, електрониката и телекомуникациите днес. Всъщност без тези правила нямаше да имате компютър, както е обичайно днес; няма да имате и програмиране, както е обичайно днес.

Истина или лъжа
Едно просто твърдение на човешкия език е или вярно, или невярно само по себе си. Ако кажа: „Аз съм висок“, това е или вярно, или невярно. Ако кажа „вие сте висок“, това е или вярно, или невярно. Ако аз съм висок, а ти си нисък и се задава въпросът дали и ти, и аз сме високи, в булевата логика трябва да се даде отговор вярно или невярно. Кое от тези двете трябва да се даде? Boole всъщност не отговори на този въпрос. Той просто измисли набор от правила, които да следваме. Добрата новина е, че когато следвате тези правила в правилния им контекст, нямате никаква неяснота. Благодарение на тези правила днес имаме компютри и програмиране. Правилата са ви дадени сега. Правилата не могат наистина да бъдат обяснени; просто ги приемаш. Правилата са под три заглавия: И, ИЛИ и НЕ.

И
Въпросът може да бъде зададен, ако и аз, и ти сме високи. Моят ръст и вашият ръст след това се комбинират от И набор от правила. Това са правилата И, които трябва да следвате:

невярно И невярно = невярно
невярно И вярно = невярно
вярно И невярно = невярно
вярно И вярно = вярно

Сега, нека високото е вярно, а ниското невярно. Това означава, че ако аз съм нисък И ти си нисък, ти и аз сме ниски. Ако аз съм нисък И ти си висок, ти и аз сме ниски; това е булевият отговор, който трябва да приемете. Ако аз съм висок И ти си нисък, и ти, и аз сме ниски. Ако аз съм висок И ти си висок, ти и аз сме високи. Всичко това са И булеви правила, които вие (читателят) просто трябва да приемете.

ИЛИ
Въпросът може да бъде зададен дали вие ИЛИ аз съм висок. След това моят ръст и вашият ръст се комбинират от набора от правила ИЛИ. Това са правилата за ИЛИ, които трябва да следвате:

невярно ИЛИ невярно = невярно
невярно ИЛИ вярно = вярно
вярно ИЛИ невярно = вярно
вярно ИЛИ вярно = вярно

Отново, нека високото е вярно, а ниското - невярно. Това означава, че ако аз съм нисък ИЛИ ти си нисък, ти ИЛИ аз съм нисък. Ако аз съм нисък ИЛИ ти си висок, ти или аз сме високи. Ако аз съм висок ИЛИ ти си нисък, ти ИЛИ аз съм висок. Ако аз съм висок ИЛИ ти си висок, ти или аз сме високи. Всичко това са булеви правила, които трябва да приемете.

НЕ
Сега, в булевата логика, съществуват само две състояния (възможни отговори). Тоест ако НЕ си висок значи си нисък. Ако НЕ сте ниски, значи сте високи; нищо друго. Това са НЕ правилата, които трябва да следвате:

НЕ невярно = вярно
НЕ вярно = невярно

Да приемем, че имате струна (или пружина), която можете да удължите (издърпате). Докато низът е в естественото си състояние, ако кажа „НЕ е къс“, вие ще го удължите; това е тълкуването. Докато низът е удължен, ако кажа „НЕ е дълъг“, ще му позволите да се свие; това е тълкуването.

Трябва да запомните всички дадени правила в различните им категории.

Повече от два операнда
В компютърния език И, ИЛИ и НЕ се наричат ​​оператори. За оператора NOT се нуждаете само от един операнд (стойност към оператор), за да получите отговор. За операторите И или ИЛИ можете да имате повече от два операнда. Предишните случаи показват два операнда за И и ИЛИ. Можете да имате три операнда за И, както следва:

невярно И невярно И невярно = невярно
невярно И невярно И вярно = невярно

Това са два реда; всеки има два оператора И. Всъщност има девет реда, когато операндите са три. С оператора AND само последният ред (деветият ред) е равен на true; всички предходни редове са неверни. Обърнете внимание, че с два операнда за И само последният ред все още е верен; всички предходни три реда са неверни. Когато операндите са четири, има 16 реда и само последният ред е верен за оператора И.

Моделът за И и моделът за ИЛИ са различни. С три операнда за два оператора OR, има също девет реда и само първият ред, този път, е false. От втория до деветия ред е вярно. Обърнете внимание, че с два операнда за ИЛИ само първият ред все още е верен; всички останали три реда са неверни. Когато операндите са четири за ИЛИ, има също 16 реда.

Операторът NOT работи само с един операнд. Невярното е вярно, а НЕвярното е невярно.

2.2 Таблица на истинността на два операнда и техните електронни компоненти

В математиката има тема, наречена алгебра. Малка част от него беше видяна в предишната глава. Има един вид алгебра, наречена булева алгебра. В булевата алгебра вярно се идентифицира с основната две цифра, която е 1, а невярното се идентифицира с основната две цифра, която е 0.

Компонентите на вътрешния компютърен модул са електронни компоненти. Системният блок на компютърната система има цифрови електронни компоненти. Операцията AND се извършва от малък електронен компонент, наречен AND gate. Операцията ИЛИ се извършва от малкия електронен компонент, наречен ИЛИ порта. Операцията NOT се извършва от малкия електронен компонент, наречен NOT gate. Твърде много от тези врати могат да бъдат в чип с интегрална схема (IC).

И Масата на истината и нейната порта
Следващата таблица дава таблицата на истината И и нейния символ И врата (малка верига):

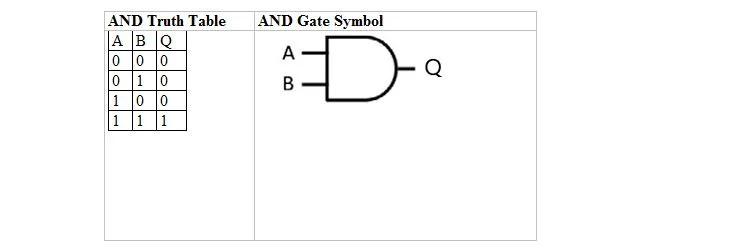
Както за И таблицата на истината, така и за нейния гейт, A, както и B са две входни променливи. Q е изходната променлива. A е или 1, или 0. B е или 1, или 0. Q е или 1, или 0. Таблицата на И истината с 1 и 0 е същата като предишното оформление (таблица) Истина/Невярно И истина. Уравнението И е:

А . B = Q

където точката (.) означава И (булева). Точката може да бъде пропусната, за да има AB = Q, което означава същото (И).

Забележка: Битовете за A и B в четирите реда, като двойки, са първите четири числа в основа две, започващи от 0 (или 00), т.е. 00, 01, 10, 11.

Следващата таблица дава таблицата на истината ИЛИ и нейния символ ИЛИ врата (малка верига):

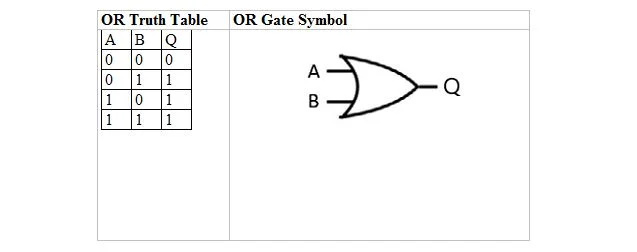
Както за таблицата на истината ИЛИ, така и за нейния гейт, A, както и B са две входни променливи. Q е изходната променлива. Таблицата на истината ИЛИ с 1 и 0 е същата като предишното оформление (таблица) на истината ИЛИ.

Уравнението ИЛИ е:

A + B = Q

Където + тук означава булево ИЛИ, а не събиране. Уравнението се чете като „A или B е равно на Q“.

Следващата таблица дава таблицата на истината NOT и нейния символ NOT gate (малка верига):

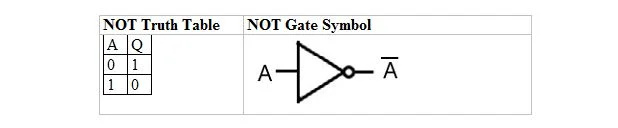
Таблицата на NOT истината или NOT gate има само един вход и един изход. Когато входът е 0, изходът е 1. Когато входът е 1, изходът е 0. Портата NOT прави един вид инверсия. Изходната променлива е същата като входната променлива, но с лента (чертана). Таблицата на истината НЕ с 1 и 0 е същата като предишното оформление (таблица) истина/истина ИЛИ.

Уравнението НЕ е:

A = Q

Където Q = A и чертата над A тук означава допълнение. Допълнението на 0 е 1, а допълнението на 1 е 0. Вратата НЕ е известна още като ИНВЕРТИРАЩА врата.

Това са основните (или коренните) таблици на истината и техните портове (малки вериги) в цифровата електроника (с булева алгебра). Другите три таблици на истината, които са дадени на следващата илюстрация, и техните портове са за удобство и се основават на предишните три таблици на истината.

Има таблица на истината и порта, които се извличат от таблицата и портата на истината И. Те се наричат ​​NAND (за NOT AND) таблица на истината и съответния NAND gate. Таблицата на истината NAND и нейният NAND порт са:

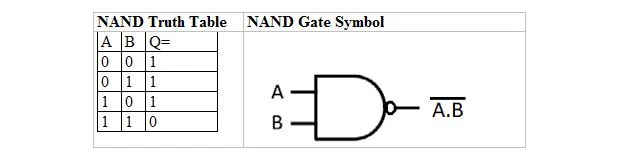
За да получите таблицата на истината NAND, отидете на изхода на таблицата на истината И и заменете всяка цифра с нейното допълнение. Допълнението на 0 е 1, а допълнението на 1 е 0. NAND портата е като И портата, но има малък кръг преди изходната линия. Уравнението на NAND е:

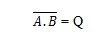
Където означава допълнението на резултата от „A“ И „B“. Лентата (надлинията) е представена на портата от малкия кръг. Имайте предвид, че точката между A и B може да бъде пропусната.

Има друга таблица на истината и порта, които се извличат от таблицата на истината и порта ИЛИ. Те се наричат ​​NOR (за НЕ ИЛИ) таблица на истината и съответния NOR gate. Таблицата на NOR истината и нейният NOR gate са:

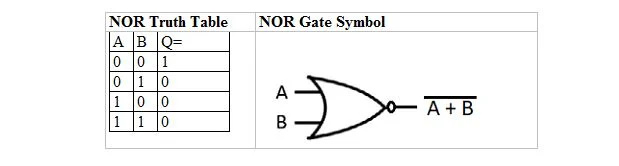
За да получите таблицата на истината ИЛИ, отидете на изхода на таблицата на истината ИЛИ и заменете всяка цифра с нейното допълнение. Допълнението на 0 е 1, а допълнението на 1 е 0. ИЛИ портата е като ИЛИ вратата, но има малък кръг преди изходния ред. Уравнението NOR е:

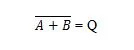
Където 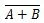означава допълнение към резултата от „А“ ИЛИ „Б“. Лентата (горната линия) е представена в портата от малкия кръг.

Изключително ИЛИ (XOR)
Таблицата на истината за портата ИЛИ е:

В нормален английски език не е ясно дали последният ред от 1 ИЛИ 1 трябва да дава 1 или 0. Така че в булевата алгебра има два вида ИЛИ таблици на истината и две съответни врати. С нормалното ИЛИ, последният ред от 1 ИЛИ 1 дава 1. Другият тип ИЛИ е изключително ИЛИ (XOR), където първите три реда са същите като първите три реда на нормално ИЛИ (включително изход). За четвъртия и последен ред обаче 1 ИЛИ 1 дава 0.

Следващата таблица дава таблицата на истината XOR и нейния символ на порта XOR (малка верига):

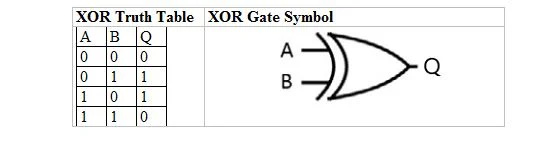
Както за таблицата на истината XOR, така и за нейния гейт, „A“, както и „B“ са две входни променливи. “Q” е изходната променлива.

Уравнението XOR е:

A ⊕ B = Q

Където ⊕ тук означава булево XOR.

Нормалното ИЛИ означава едно или и двете. Изключително ИЛИ означава строго или а не и двете.

2.3 Булеви постулати

Постулатите са предположения, въз основа на които се правят определени заключения. Има десет булеви постулата, които се коренят от уравненията И, ИЛИ и НЕ (таблици на истината). Тези уравнения се наричат ​​още функции. Основните функции се копират, както следва:

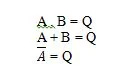
Това са основните функции (уравнения) в булевата алгебра. Следните други три (функции) уравнения не са фундаментални функции:

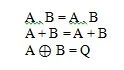
Въпреки че последната функция тук е странна, тя не се счита за основна функция.

Булевите постулати са както следва:

От функция И
1) 0 . 0 = 0
двайсет 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1

От функция ИЛИ
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

От функция НЕ
9) 0 = 1
10) 1 = 0

Забележка: Тези постулати са само редовете в таблиците за истинност И, ИЛИ и НЕ, които са изразени по независим начин. Читателят трябва да запомни дадените постулати.

2.4 Булеви свойства

Свойството е подобна характеристика на нещо. Булевите свойства са уравнения, които се извличат от булевите постулати. В този раздел свойствата просто се дават без техните производни и след това се използват след това. Има двадесет и пет от свойствата, които са групирани под десет заглавия, както следва:

Свойства на функцията И

Свойство 1:

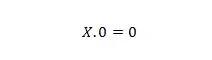
Където X може да бъде 1 или 0. Това означава, че независимо какво е X, резултатът винаги е 0.

Забележка: Променливата не трябва непременно да бъде A или B или C или D. Променливата може да бъде W или X или Y или Z или всяка друга буква.

Свойство 2:

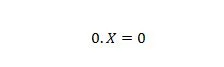
Където X може да бъде 1 или 0. Обърнете внимание, че разликата между свойство 1 и свойство 2 е, че от лявата страна на знака за равенство на двете уравнения позициите на X и 0 са разменени.

Свойство 3:

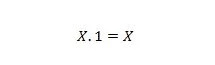
Ако X е 0, тогава 0. 1 = 0. Ако X е 1, тогава 1. 1 = 1.

Свойство 4:

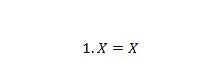
Ако X е 0, тогава 1. 0 = 0. Ако X е 1, тогава 1. 1 = 1. Обърнете внимание, че разликата между свойство 3 и свойство 4 е, че от лявата страна на двете уравнения, позициите на X и 1 са разменени.

Свойства на функцията ИЛИ

Свойство 5:

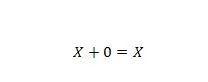
Където X може да бъде 1 или 0. Това означава, че ако X е 0, резултатът е 0. Ако X е 1, резултатът е 1.

Свойство 6:

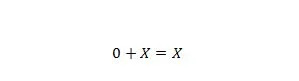
Където X може да бъде 1 или 0. Обърнете внимание, че разликата между свойство 5 и свойство 6 е, че от лявата страна на двете уравнения позициите на X и 0 са разменени.

Свойство 7:

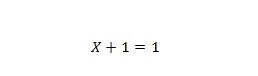
Ако X е 0, тогава 0 + 1 = 1. Ако X е 1, тогава 1 + 1 = 1.

Свойство 8:

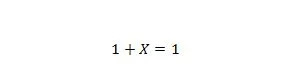
Ако X е 0, тогава 1 + 0 = 1. Ако X е 1, тогава 1 + 1 = 1. Обърнете внимание, че разликата между свойство 7 и свойство 8 е, че от лявата страна на двете уравнения, позициите на X и 1 са разменени.

Свойства, отнасящи се до комбинацията на променлива със себе си или нейното допълнение

Свойство 9:

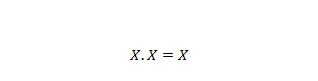
Тоест: ако X е 0, тогава 0 . 0 = 0. Ако X е 1, тогава 1 . 1 = 1.

Свойство 10:

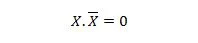
Тоест: ако X е 0, тогава 0. 1 = 0. Ако X е 1, тогава 1. 0 = 0.

За последователни променливи това свойство става:

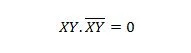
Свойство 11:

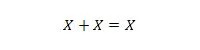
Тоест: ако X е 0, тогава 0 + 0 = 0. Ако X е 1, тогава 1 + 1 = 1 (от нормално ИЛИ).

Свойство 12:

Тоест: ако X е 0, тогава 0 + 1 = 1. Ако X = 1, тогава 1 + 0 = 1.

Тоест: ако X е 0, тогава 0 + 1 = 1. Ако X = 1, тогава 1 + 0 = 1.

Двойно допълване

Свойство 13:

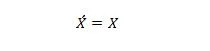
Когато X от лявата страна е 0, X от дясната страна става 0. Когато X от дясната страна е 1, X от лявата страна става 1. С други думи, двойните допълнения връщат първоначалната стойност.

Комутативно право

Свойство 14:

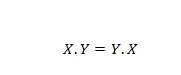
Това означава, че размяната на първия и втория операнд за оператора И от лявата страна на знака за равенство няма значение; отговорът все още е същият след размяната от лявата страна. Това уравнение може да бъде написано с пропуснати точки като: XY = YX.

Свойство 15:

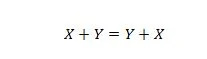
Обяснението тук е същото като в предишното И, но е за оператора ИЛИ.

Разпределителен закон

Свойство 16:

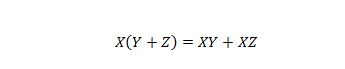
Тук има три променливи: X, Y и Z. Всяка променлива може да бъде 1 или 0. От лявата страна на символа за равенство, скобите означават първо да се оцени какво има в тях. След това И е резултатът с X. Дясната страна казва, че X И Y заедно, ИЛИ X И Z заедно, са същите като лявата страна. Обърнете внимание, че операторът за точка за И се пропуска навсякъде; и обединените променливи все още означават И.

Свойство 17:

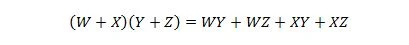
Това свойство е разширение на свойство 16 с добавената променлива на W.

Асоциативен закон

Свойство 18:

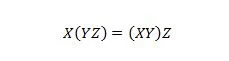
Скобите означават първо да се оцени какво е в скобите. И така, за израза от лявата страна, ако Y със Z първо се използва AND, а X е AND с резултата, тогава този краен резултат от лявата страна е същият като крайния резултат отдясно -hand-side, където X с Y се подлага първо на AND преди AND на резултата с Z. Имайте предвид, че точките са пропуснати в уравнението.

Свойство 19:

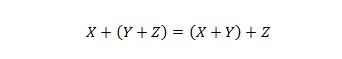
Това свойство се обяснява по подобен начин като свойство 18, но операторът OR се използва вместо оператора AND. Операторът ИЛИ + никога не се пропуска от булев израз за по-голяма простота. От друга страна, операторът И може да бъде пропуснат и двете променливи могат да бъдат обединени.

Абсорбция

Свойство 20:

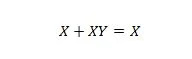
С това уравнение, без значение какво е Y, дясната страна винаги ще бъде X (абсорбирано).

Свойство 21:

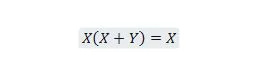
Също така, с това уравнение, без значение какво е Y, дясната страна винаги ще бъде X (погълнато). Това свойство 21 е същото като със свойство 20, което е:

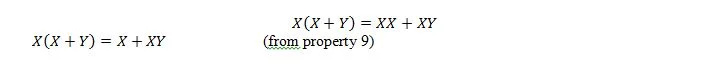
Тук използваме закона за разпределение и факта, че X.X = X на свойство 9.

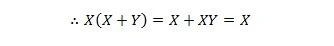
Идентичност

Свойство 22:

Това означава, че за израза X + Y, допълнението на X пред Y не променя израза.

Свойство 23:

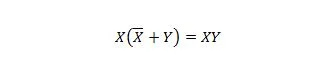
Това означава, че за XY израза допълнението на X ИЛИ с Y в скоби, което се прави първо, не променя XY израза.

Законът на ДеМорган

Свойство 24:

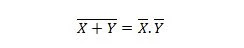
Това означава, че NOR (НЕ ИЛИ) порта има същия резултат като NOT на двата входа преди да ги AND.

Свойство 25:

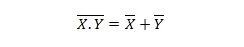
Това означава, че порта NAND (НЕ И) има същия резултат като БЕЗ двата входа преди ИЛИ.

Предоставените илюстрации са 25-те свойства. Те могат да бъдат доказани чрез заместване на всички различни възможни стойности на 1 и 0 във всеки израз от лявата страна, за да се види дали изразът (или резултатът) от дясната страна е получен. Доказателствата са оставени като упражнение за читателя.

2.5 Опростяване на съставни изрази

Следните две функции са еднакви:

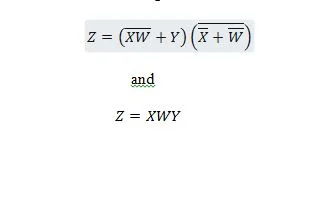
Z е изходът, а X, W и Y са входовете. Първият се нуждае от NAND порта, ИЛИ порта, И порта, две НЕ порти, ИЛИ порта и ИЛИ порта. Вторият се нуждае само от две И врати. Първото е уравнение със съставен израз от дясната страна, който е опростен (редуциран) до единствения десен израз за второто уравнение.

Опростяването или намаляването води до по-малък брой порти, за да се приложи същата функция като верига. Такава по-малка схема може да бъде част от интегрална схема (IC) или да бъде самостоятелна схема на повърхността на дънната платка на компютъра.

Когато функция (уравнение) пристигне в процеса на проектиране, трябва да се извърши опростяване, за да се намали броят на портите и да се получи по-евтина схема. Опростяването изисква използването на едно или повече от предишните двадесет и пет булеви свойства.

Пример 2.51:

Редуцирайте уравнението:

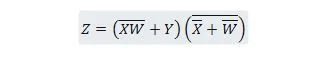
Забележка: Две скоби една до друга означават, че скобите са поставени с И (точката между тях по избор не е написана).

Решение:
За решенията обосновката (причината) за всяка стъпка е дадена отдясно на стъпката, в скоби. Читателят трябва да прочете всяка стъпка и нейната обосновка. Читателят трябва също да се позовава на предишните свойства, докато чете стъпките за намаляване на функцията.

Пример 2.52:

Опростете:

2.6 Минимална сума от продукти

Следните две функции са еднакви:

И двата десни израза на двете уравнения се казва, че са под формата на сума от продукти (SP). Казва се, че експресен израз е във формата на сума на продукта, ако няма скоби. Очевидно е, че първата функция (уравнение) се нуждае от повече врати от втората функция.

Първият десен израз все още може да бъде намален, за да се получи втората функция. Вторият израз от дясната страна не може да бъде опростен повече и все пак да бъде изразен като сума от продукти („добавяне“ на членове). Вторият израз от дясната страна всъщност не може да бъде опростен повече. И така, казва се, че е във формата за минимална сума от продукти (MSP).

Пример 2.61:
Пренесете следната функция първо във формуляра Сума от продукти и след това във формуляра Минимална сума от продукти.

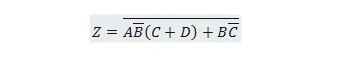
Решение:
При решаване на проблеми като този, едно или повече от предишните двадесет и пет свойства трябва да се използват, както е илюстрирано в това решение:

2.6 Минимална сума от продукти

Следните две функции са еднакви:

И двата десни израза на двете уравнения се казва, че са под формата на сума от продукти (SP). Казва се, че експресен израз е във формата на сума на продукта, ако няма скоби. Очевидно е, че първата функция (уравнение) се нуждае от повече врати от втората функция.

Първият десен израз все още може да бъде намален, за да се получи втората функция. Вторият израз от дясната страна не може да бъде опростен повече и все пак да бъде изразен като сума от продукти („добавяне“ на членове). Вторият израз от дясната страна всъщност не може да бъде опростен повече. И така, казва се, че е във формата за минимална сума от продукти (MSP).

Пример 2.61:
Пренесете следната функция първо във формуляра Сума от продукти и след това във формуляра Минимална сума от продукти.

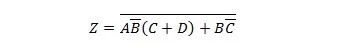
Решение:
При решаване на проблеми като този, едно или повече от предишните двадесет и пет свойства трябва да се използват, както е илюстрирано в това решение:

Този последен израз е във формуляр за сума от продукти (SP), но не и във формуляр за минимална сума от продукти (MSP). На първата част от въпроса е отговорено. Решението за втората част е следното:

Тази последна опростена функция (уравнение) е във форма на MSP и се нуждае от по-малък брой порти за внедряване в сравнение със съответната форма SP. Запомнете: SP означава сума от продукти, докато MSP означава минимална сума от продукти.

Пример 2.62:
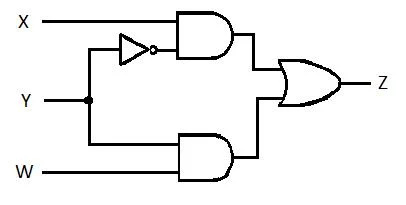
Следващата верига има входове X, Y и W, а Z е изходът. Изгответе функцията за сбор от продукти (SP) (привидна минимална функция за сбор от продукти) за Z. След това изгответе истинската по-намалена (минимизирана) сума от продукти (MSP). След това внедрете веригата MSP (начертайте стробиращата мрежа MSP).

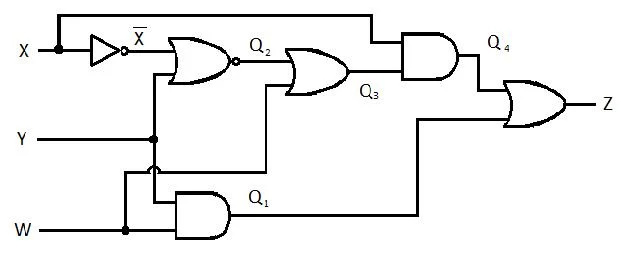
Фиг. 2.61 Стробираща верига

Решение:
Преди да започне процесът на опростяване, изразът за Z трябва да бъде получен по отношение на X, Y и W. Вижте тази примерна илюстрация от диаграмата:

Това е изразът на Z по отношение на X, Y и W. След това може да се извърши опростяването до очевиден MSP. Очевидно MSP е SP.

Това последно уравнение (функция) е в SP форма. Не е вярна минималната сума на продуктите (все още не е MSP). Така че намаляването (минимизирането) трябва да продължи.

Това последно уравнение (функция) е истинска минимална сума от продукти (MSP). И минималната сума от продукти (истинско минимизиране) стробираща верига е:

Фигура 2.62 MSP стробираща верига

Коментирайте
От анализа в този раздел може да се види, че не е ясно дали сумата от продукти е минималната сума от продукти или не. SP не е много полезно. Това е MSP, което е много полезно. Има сигурен начин за получаване на MSP; това е да използвате картата Karnaugh. Karnaugh Map е извън обхвата на този онлайн курс за кариера.

2.7 Проблеми

На читателя се препоръчва да реши всички задачи в дадена глава, преди да премине към следващата глава.

1. Създайте таблиците за истинност И, ИЛИ и НЕ със съответните им гейтове.
2. Запишете десетте булеви постулата в различните им категории, като наименувате категориите.
3. Без обяснение запишете двадесет и шестте свойства на булевата алгебра в различните им категории, като наименувате категориите.
4. Редуцирайте уравнението, като използвате булевите свойства и цитирате използваните категории.



5. Редуцирайте уравнението, като използвате булевите свойства и цитирате използваните категории.



6. Използвайки булевите свойства и цитирайки използваните категории, редуцирайте следното уравнение – първо до сума от продукти и след това до минимална сума от продукти:



7. Използвайки булевите свойства и цитирайки използваните категории, редуцирайте следното уравнение – първо до сума от продукти и след това до минимална сума от продукти: